Topology has two particularly often realized subcases in applications: the manifold and the graph. Manifolds are continuum entities while graphs are discrete ones. In this sense, our Topological program here starts with overlap with our Geometry program (topological and differentiable manifolds). And our Combinatorics program https://wordpress.com/page/conceptsofshape.space/951 (Graph Theory constitutes a large portion of this subject to date).

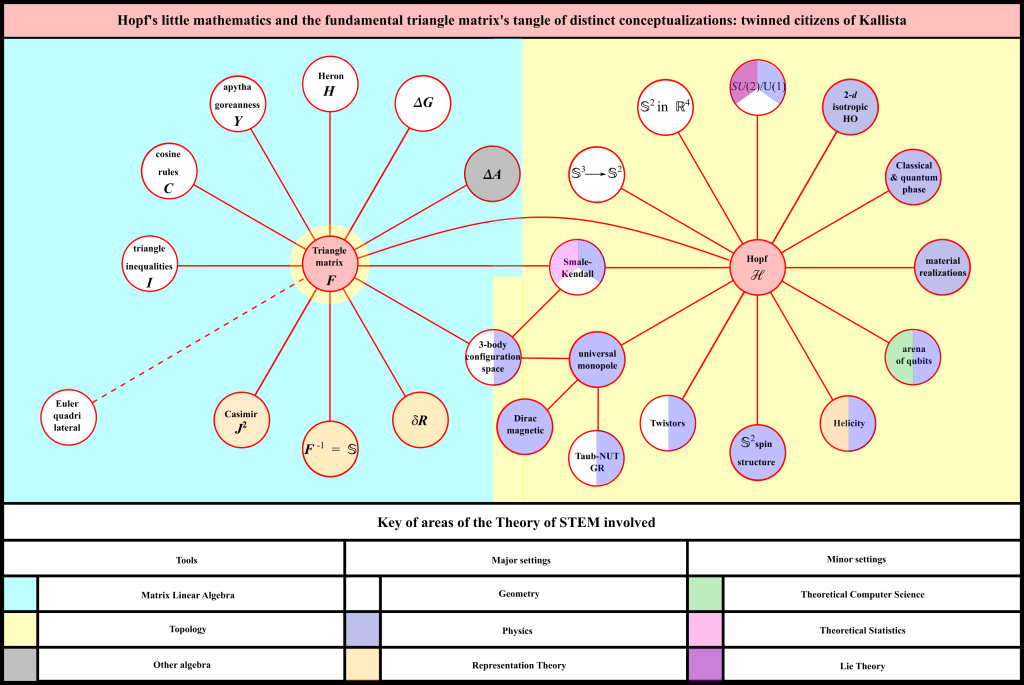
The first more fully topological subject matter that we are studying here is the Hopf map from the 3-sphere to the 2-sphere, and its corresponding fibration and principal fibre bundle. Here are some of the conceptualizations leading to this, colour-coded as regards which parts of the Theory of STEM that they belong to.

Our name for the above is Hopf’s little mathematics, including Smale’s Little Theorem and Kendall’s Little Theorem. All of these `littles’ are in the context of the generalization to S^(2n + 1) mapping to CP^n, where the S is a sphere of the indicated dimension, and CP stands for complex-projective space.

In this way, our Flat Geometry subprogram’s robustness test for which triangle results hold for quadrilaterals becomes part of our Applied Topology’s robustness test for little within generalized. The connection being that Smale and Kendall’s generalized Theorems pick out CP^(N – 2) as the shape spaces modulo similarities of the N-gons. For triangles, the accidental relation CP^1 = S^2 strikes! Leaving quadrilaterals’ CP^2 as the first nontrivially complex-projective case. Which is far more generic in many ways that our Geometry and Applied Topology programs document!

The follwing Summer School starts on August 9 2024.

See https://institute-theory-stem.org/first-write-up-from-the-hopf-map-32-times-in-geometry-and-physics-summer-school-2024/ for the introductory seminar on the Hopf map.