The first few installments of this shall be drawn from (multi-)linear algebra, flat geometry, differential geometry, classical physics, and general relativity. Aside from algebraic and geometric perspectives, combinatorial and representation-theoretic aspects shall also be emphasized. Expect the first few small webpages on this to start to appear in 2026.

(Multi-)Linear Algebra

Let’s start at the very beginning. A very good place to start! For Multi-Linear algebra, this would surely be Linear Algebra. And so here are a few resources on Linear Algebra. These are sample chapters from a book by one of us, to be called Linear Mathematics. Vector Spaces, Linear Methods and Tensors throughout STEM wordpress.com/page/conceptsofshape.space/3406/ 

Chapter 0. https://wordpress.com/page/conceptsofshape.space/1597

Chapter 1. What is a Vector? https://wordpress.com/page/conceptsofshape.space/1584

Chapter 2. Lines, Planes, Flats and Hyperplanes. https://wordpress.com/page/conceptsofshape.space/1586

Chapter 3. Matrices. https://wordpress.com/page/conceptsofshape.space/1588

Chapter 4. Square Transformation Matrices. https://wordpress.com/page/conceptsofshape.space/1632

Chapter 6. Linear-Algebraic Systems of Inequalities. https://wordpress.com/page/conceptsofshape.space/1627

Chapter 9. Linear Spans-and-Bases. https://wordpress.com/page/conceptsofshape.space/1612

Chapter 10. Affine Spaces. https://wordpress.com/page/conceptsofshape.space/1601

Chapter 11. Convex Subsets and Functions. https://wordpress.com/page/conceptsofshape.space/1606

Chapter 17. NEW as of 01/01/2026 The Rank-Nullity Theorem https://wordpress.com/page/conceptsofshape.space/3992

Paper counterparts of 5 other Chapters shall be linked to here within 2026.

Namely the first published version of the Periodically Updating Review “Eigentheory of Symmetric Matrices” by E. Anderson and K. Everard.

And 1 Chapter’s worth of “Other arenas of Linear-Algebraic structures”.

As a common source for what these shall be like, consult E. Anderson, “Eigentheory of Combinatorial Matrices: a More General Setting for the CoM-Relative Split”, Ann. Inst. Theory STEM 1 6 (2025), institute-theory-stem.org/annals-of-the-institute-of-stem/ . The first 20 or so pages are in the style that “Eigentheory of Symmetric Matrices” considerably generalizes upon. While “Other arenas of Linear-Algebraic structures” will be pinning graphs and orders on various Linear Algebra structures much like the last half dozen figures of this common source uses.

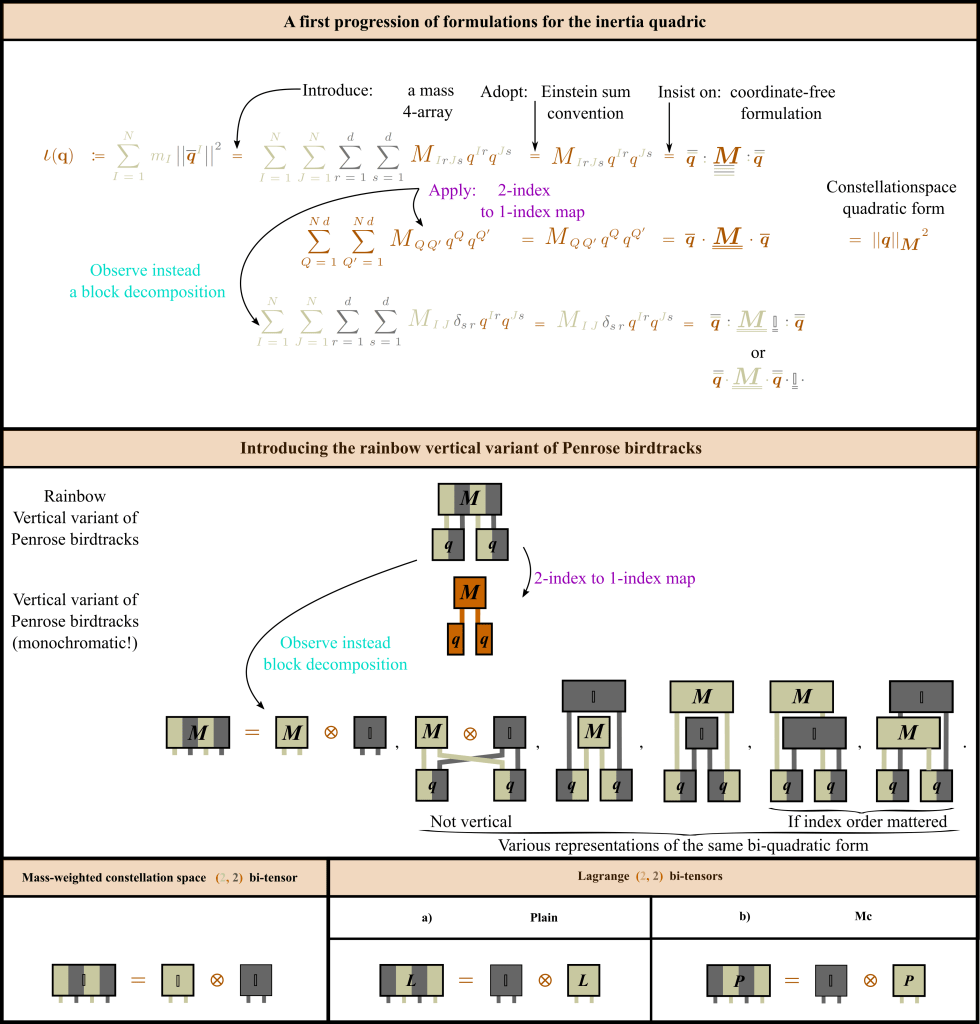
Let’s start at the very beginning. A very good place to start! For tensors, we will present a long suite of types of notation. Moving towards the Penrose birdtrack or its close ally and often alias the tensor network. As a stand-in for what we shall exhibit here, have the following for now. Which is the N-Body problem case’s first figure!

Tensors