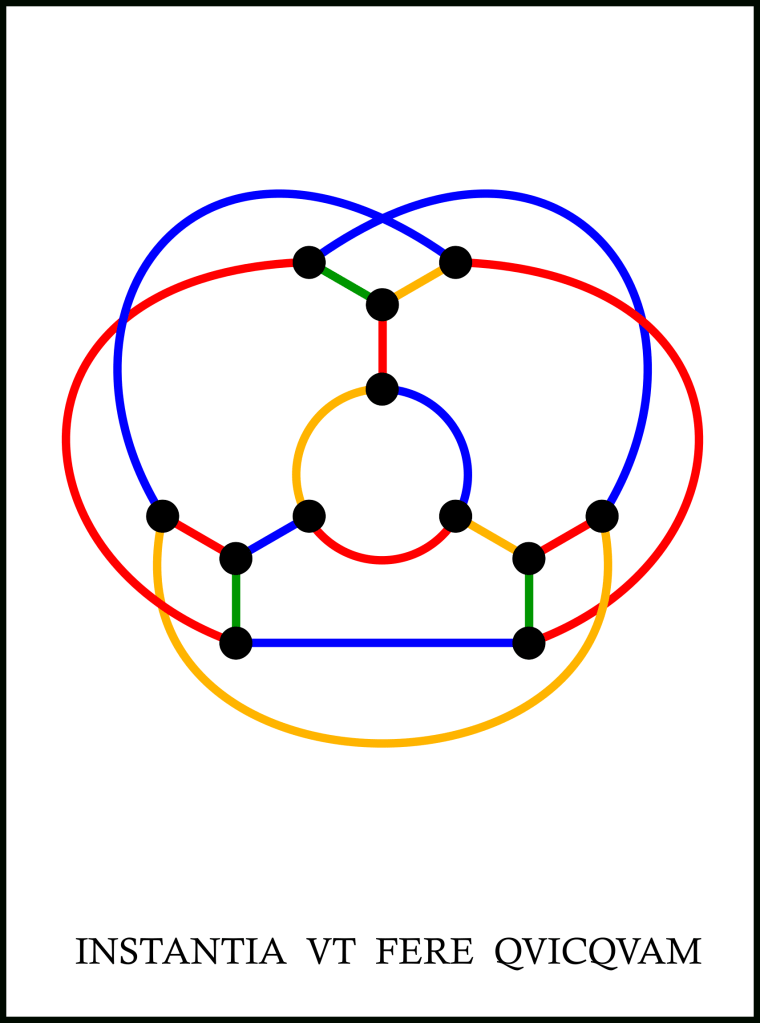
Give a conceptual description of how I am related to Riddle 3’s graph. What is my edge-chromatic number? And what is my crossing number?

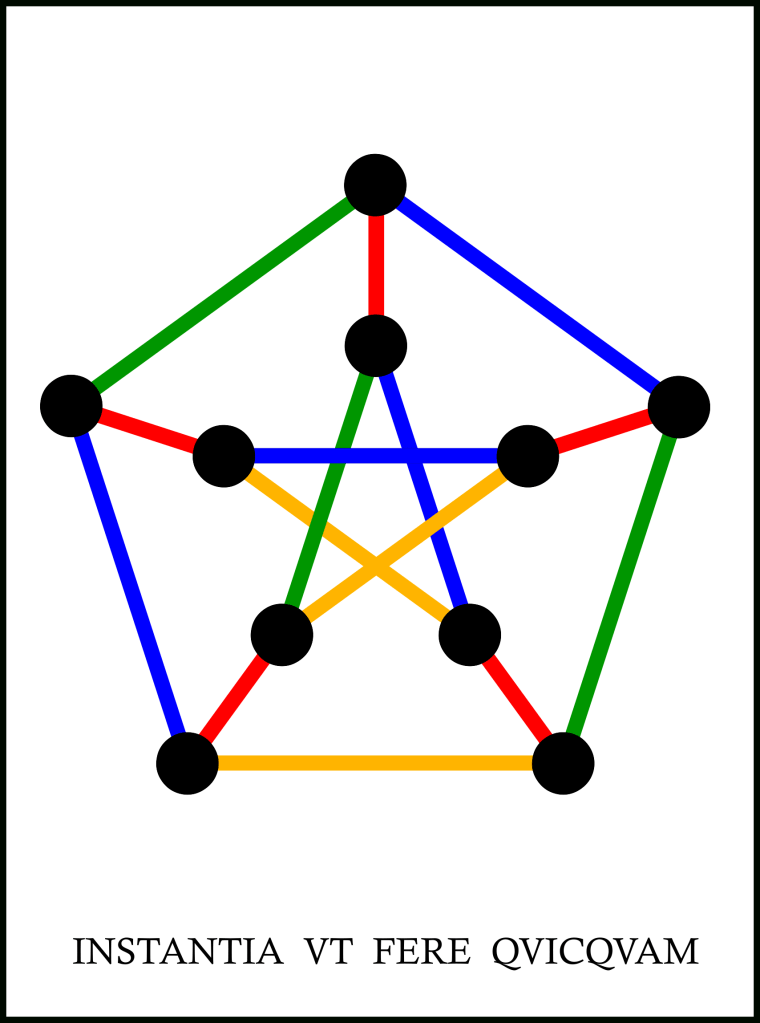
How else can I be drawn? What is my crossing number? That is, what is the minimum number of crossings between my edges with which I can be drawn in a plane? (As represented by, say, the piece of paper on which you try to solve this riddle!)

How else can I be edge-coloured? This is to be such that no two edges emanating from the same vertex have the same colour! What is my edge chromatic number? That is, what is the minimum number of colours with which I can be edge-coloured?

Show that I am the same graph as in Riddle 1. This includes you determining both of the following. For this purpose, what is a sufficient definition of ‘graph’? And a sufficient definition of ‘the same’?

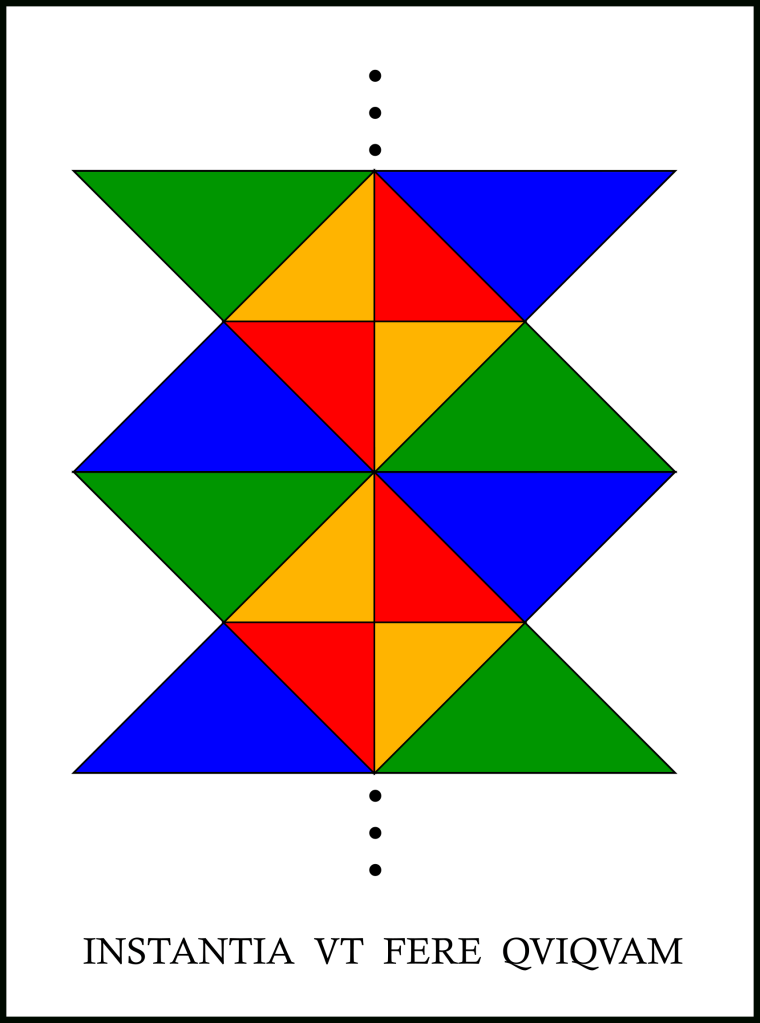
What does the motto mean? Why am I a depiction of this motto? What interesting properties do I have? What name have I hitherto gone by? What are truer names for me?

What interesting properties do I have? What name have I hitherto gone by? What are truer names for me? What does the motto mean? And why am I a depiction of this motto?